高等数学同济大学第七版习题答案_复习笔记pdf

五、极限运算法则

1极限运算法则相关定理

（1）定理1

两个无穷小的和是无穷小，有限个无穷小之和也是无穷小。

（2）定理2

有界函数与无穷小的乘积是无穷小。

①推论1：常数与无穷小的乘积是无穷小。

②推论2：有限个无穷小的乘积是无穷小。

（3）定理3

如果limf（x）＝A，limg（x）＝B，则

①lim[f（x）±g（x）]＝limf（x）±limg（x）＝A±B；

②lim[f（x）·g（x）]＝limf（x）·limg（x）＝A·B；

③若又有B≠0，则lim（f（x）/g（x））＝limf（x）/limg（x）＝A/B

a．推论1：如果limf（x）存在，而c为常数，则lim[cf（x）]＝climf（x）；

b．推论2：如果存在，而n是正整数，则lim[f（x）]ⁿ＝[limf（x）]ⁿ。

六、极限存在准则及两个重要极限

1极限存在准则

（1）夹逼准则

①夹逼准则1

如果数列{x_n}，{y_n}及{z_n}满足下列条件：

a．从某项起，即∃n₀∈N_＋，当n＞n₀时，有y_n≤x_n≤z_n；

b．，则数列{x_n}的极限存在，且。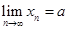

②夹逼准则2

a．当x∈U°（x₀，r）（或|x|＞M）时，g（x）≤f（x）≤h（x）；

b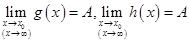．，则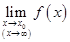存在，且等于A。

（2）单调有界准则

单调有界数列必有极限。

（3）左极限存在准则

设函数f（x）在点x₀的某个左邻域内单调并且有界，则f（x）在x₀的左极限f（x₀^－）必定存在。

（4）柯西极限存在准则

数列{x_n}收敛的充分必要条件是：对于任意给定的正数ε，存在正整数N，使得当m＞N，n＞N时，有|x_n－x_m|＜ε。

（7）幂指函数的极限

一般地，对于形如u（x）^v（x）（u（x）＞0，u（x）≠1）的函数（通常称为幂指函数），如果limu（x）＝a＞0，limv（x）＝b，limu（x）^v（x）＝a^b。

注：这里三个lim都表示在同一自变量变化过程中的极限。

4有关sinx，x，tanx的不等式

sinx＜x＜tanx，∀x∈（－π/2，0）或（0，π/2）

十、闭区间上连续函数的性质

1函数f（x）在闭区间[a，b]上连续

如果函数f（x）在开区间（a，b）内连续，在右端点b左连续，在左端点a右连续，则函数f（x）就是在闭区间[a，b]上连续。

2闭区间上连续函数的性质（见表1-4）

表1-4 闭区间上连续函数的性质

3一致连续性

（1）一致连续与连续的关系

如果函数f（x）在区间I上一致连续，则f（x）在区间I上一定连续；当f（x）在区间I上连续，f（x）在区间I上不一定一致连续。

（2）一致连续性定理

如果函数f（x）在闭区间[a，b]上连续，则它在该区间上一致连续。