找课后习题答案,就上大学教材课后答案网!
查看完整版: 高等数学第六版下册课后习题答案
高等数学第六版下册课后习题答案
第1章 函数与极限
1.1 复习笔记
1.2 课后习题详解
1.3 考研真题详解
第2章 导数与微分
2.1 复习笔记
2.2 课后习题详解
2.3 考研真题详解
第3章 微分中值定理与导数的应用
3.1 复习笔记
3.2 课后习题详解
3.3 考研真题详解
第4章 不定积分
4.1 复习笔记
4.2 课后习题详解
4.3 考研真题详解
第5章 定积分
5.1 复习笔记
5.2 课后习题详解
5.3 考研真题详解
第6章 定积分的应用
6.1 复习笔记
6.2 课后习题详解
6.3 考研真题详解
第7章 微分方程
7.1 复习笔记
7.2 课后习题详解
7.3 考研真题详解
 第1章 函数与极限
第1章 函数与极限
 1.1 复习笔记
1.1 复习笔记
一、映射与函数
1.集合
(1)集合概念
集合(简称集)是指具有某种特定性质的事物的总体,组成这个集合的事物称为该集合的元素(简称元)。常用大写拉丁字母A,B,C,…表示集合,用小写拉丁字母a,b,c,…表示集合的元素。
如果a是集合A的元素,就说a属于A,记作a∈A;如果a不是集合A的元素,就说a不属于A,记作a A。
A。
一个集合,若它只含有有限个元素,则称为有限集;不是有限集的集合称为无限集。
(2)表示集合的方法通常有以下两种:
①列举法,就是把集合的全体元素一一列举出来表示;
②描述法,若集合M是由具有某种性质P的元素x的全体所组成的,就可表示成M={x|具有性质P}。
(3)常见的集合
①空集,指不包含任何元素的集合,记为φ;
②非负整数集,全体非负整数即自然数的集合,记作N,即N={0,1,2,…,n,…};
③正整数集,全体正整数的集合,记作 ,即
,即 ={1,2,3,…,n,…};
={1,2,3,…,n,…};
④整数集,全体整数的集合,记作Z,即Z={…,-n,…,-2,-1,0,1,2,…,n,…};
⑤有理数集,全体有理数的集合,记作Q,即Q={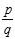 ∈z,q∈
∈z,q∈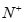 且P与q互质};
且P与q互质};
⑥实数集,全体实数的集合,记作R,R为排除数0的实数集, 为全体正实数的集合。
为全体正实数的集合。
(4)集合的关系
①包含关系
设A、B是两个集合,如果集合A的元素都是集合B的元素,则称A是B的子集,记作A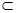 B(读作A包含于B)或B
B(读作A包含于B)或B A(读作B包含A)。规定空集φ是任何集合A的子集,即φ
A(读作B包含A)。规定空集φ是任何集合A的子集,即φ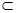 A。
A。
若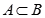 且
且 ,则称A是B的真子集,记作
,则称A是B的真子集,记作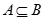 (读作A真包含于B)。
(读作A真包含于B)。
②等价关系
若集合A与集合B互为子集,即A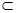 B且B
B且B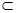 A,则称集合A与集合B相等,记作A=B。
A,则称集合A与集合B相等,记作A=B。
(5)集合的运算
①并、交、差
a.并集
设A、B是两个集合,由所有属于A或者属于B的元素组成的集合,称为A与B的并集(简称并),记作 ,即
,即 。
。
b.交集
由所有既属于A又属于B的元素组成的集合,称为A与B的交集(简称交),记作 ,即
,即

。
c.差集
由所有属于A而不属于B的元素组成的集合,称为A与B的差集(简称差),记作A\B,即
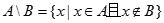 。若集合I为全集或基本集,称I\A为A的余集或补集,记作AC。
。若集合I为全集或基本集,称I\A为A的余集或补集,记作AC。
②集合的运算法则
设A、B、C为任意三个集合,则有下列法则成立:

③笛卡尔积
设A、B是任意两个集合,在集合A中任意取一个元素x,在集合B中任意取一个元素y,组成一个有序对(x,y),把这样的有序对作为新的元素,它们全体组成的集合称为集合A与集合B的笛卡尔积,记为A×B,即
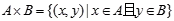
。
(6)区间和邻域
①区间
a.开区间
设a和b都是实数,且a<b,数集{x|a<x<b}称为开区间,记作(a,b),即(a,b)={x|a<x<b}。其中a和b称为开区间(a,b)的端点,这里 ,
,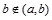 。
。
b.闭区间
数集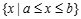 称为闭区间,记作[a,b],即
称为闭区间,记作[a,b],即 。其中a和b称为闭区间[a,b]的端点,这里a∈[a,b],b∈[a,b]。
。其中a和b称为闭区间[a,b]的端点,这里a∈[a,b],b∈[a,b]。
c.半开区间
定义 ,
,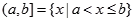 ,[a,b)和(a,b]都称为半开区间。前者也称为前闭后开区间,后者也称为前开后闭区间。
,[a,b)和(a,b]都称为半开区间。前者也称为前闭后开区间,后者也称为前开后闭区间。
d.区间长度
对于有限区间(a,b),数b-a称为区间长度。对于无限区间,引进记号十∞(读作正无穷大)及-∞(读作负无穷大),其区间长度为∞。全体实数的集合R也可记作(-∞,+∞),它也是无限区间。
查看完整版: 高等数学第六版下册课后习题答案
高等数学第六版下册课后习题答案
相关资料推荐
下一篇:


