找课后习题答案,就上大学教材课后答案网!
查看完整版: 同济大学高等数学第七版下册课后题答案
同济大学高等数学第七版下册课后题答案
本书是同济大学数学系《高等数学》(第7版)教材的学习辅导书,主要包括以下内容:
1.整理名校笔记,浓缩内容精华。在参考了国内外名校名师讲授该教材的课堂笔记基础上,复习笔记部分对该章的重难点进行了整理,因此,本书的内容几乎浓缩了该教材的知识精华。
2.解析课后习题,提供详尽答案。本书参考了该教材的国内外配套资料和其他教材的相关知识对该教材的课(章)后习题进行了详细的分析和解答,并对相关重要知识点进行了延伸和归纳。
3.挑选考研真题,总结出题思路。本书挑选了部分名校的相关考研真题,总结出题思路,有利于强化对重要知识点的理解。
 第1章 函数与极限
第1章 函数与极限
 1.1 复习笔记
1.1 复习笔记
一、映射与函数
1函数
(1)函数的性质(见表1-1)
表1-1 函数的性质
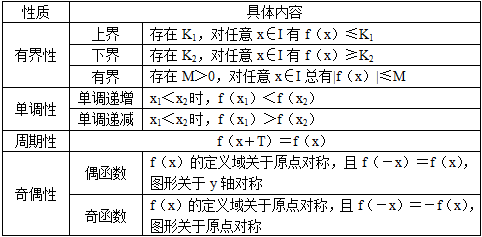
(2)反函数与复合函数
①反函数的特点
a.函数f和反函数f-1的单调性一致。
b.f的图像和f-1的图像关于直线y=x对称。
②复合函数
g与f能构成复合函数f°g的条件是:f的定义域与g的值域的交集不能为空集。
(3)函数的运算
设函数f(x),g(x)的定义域为Df,Dg,且定义域有交集为D,则可定义这两个函数的下列运算
和(差)f±g:(f±g)(x)=f(x)±g(x),x∈D。
积f·g:(f·g)(x)=f(x)·g(x),x∈D。
商f/g:(f/g)(x)=f(x)/g(x),x∈D\{x|g(x)=0,x∈D}。
(4)初等函数
5类基本初等函数:幂函数、指数函数、对数函数、三角函数、反三角函数。
二、数列的极限
1数列极限的定义
数列{xn}收敛于a⇔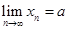 ⇔∀ε>0,∃正整数N,当n>N时,有|xn-a|<ε。
⇔∀ε>0,∃正整数N,当n>N时,有|xn-a|<ε。
数列{xn}是发散⇔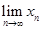 不存在。
不存在。
2收敛数列的性质
(1)唯一性
如果数列{xn}收敛,则它的极限唯一。
(2)有界性
如果数列{xn}收敛,则数列{xn}一定有界。
①有界数列:存在正数M,使得对于一切xn都满足不等式|xn|≤M。
②无界数列:不存在正数M,使得对于一切xn都满足不等式|xn|≤M。
(3)保号性
如果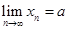 ,且a>0(或a<0),则存在正整数N>0,当n>N时,都有xn>0(或xn<0)。
,且a>0(或a<0),则存在正整数N>0,当n>N时,都有xn>0(或xn<0)。
推论:如果数列{xn}从某项起有xn≥0(或xn≤0)且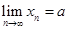 ,则a≥0(或a≤0)。
,则a≥0(或a≤0)。
(4)收敛数列与其子数列间的关系
①如果数列{xn}收敛于a,则它的任一子数列也收敛,且极限也是a。
②如果数列{xn}有两个子数列收敛于不同的极限,则数列{xn}是发散的。
③一个发散的数列也可能有收敛的子数列。
相关资料推荐


