找课后习题答案，就上大学教材课后答案网！
查看完整版：
高数教材同济第六版课后题答案
第8章 空间解析几何与向量代数
8.1 复习笔记
8.2 课后习题详解
8.3 考研真题详解
第9章 多元函数微分法及其应用
9.1 复习笔记
9.2 课后习题详解
9.3 考研真题详解
第10章 重积分
10.1 复习笔记
10.2 课后习题详解
10.3 考研真题详解
第11章 曲线积分与曲面积分
11.1 复习笔记
11.2 课后习题详解
11.3 考研真题详解
第12章 无穷级数
12.1 复习笔记
12.2 课后习题详解
12.3 考研真题详解
第8章 空间解析几何与向量代数
8.1 复习笔记
在平面解析几何中，通过坐标法把平面上的点与一对有次序的数对应起来，把平面上的图形和方程对应起来，从而可以用代数方法来研究几何问题。空间解析几何也是按照类似的方法建立起来的。
一、向量及其线性运算
1．向量概念
（1）向量
客观世界中有这样一类量，它们既有大小，又有方向，例如位移、速度、加速度、力、力矩等等，这一类量叫做向量（或矢量）。在数学上，常用一条有方向的线段，即有向线段来表示向量。有向线段的长度表示向量的大小，有向线段的方向表示向量的方向。以A为起点、B为终点的有向线段所表示的向量记
。有时也用一个黑体字母（书写时，在字母上面加箭头）来表示向量，例如a、r、v、F或
、
、
、
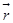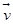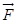等等。
（2）向量的大小和方向
由于一切向量的共性是都有大小和方向，因此在数学上只研究与起点无关的向量，并称这种向量为自由向量（简称向量），即只考虑向量的大小和方向。
由于只讨论自由向量，所以如果两个向量a和ｂ的大小相等，且方向相同，就认为向量a和ｂ是相等的，记作a＝ｂ。这就是说，经过平行移动后能完全重合的向量是相等的。
（3）向量的模
向量的大小叫做向量的模。向量、a、
的模依次记作
、
、
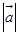。模等于1的向量叫做单位向量。模等于零的向量叫做零向量，记作0或
。零向量的起点和终点重合，它的方向可以看做是任意的。
（4）向量的夹角
设有两个非零向量a，b，任取空间一点O，作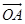
＝a，
＝b，规定不超过
的
AOB（设
＝AOB，0≤≤）称为向量a与b的夹角（图8-1），记作（a，b）或（b，a），即（a，b）＝。如果向量a与b中有一个是零向量，规定它们的夹角可以在0到之间任意取值。
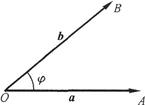
图8-1 非零向量a，b
如果（a，b）＝0或，就称向量a与b平行，记作a//b。如果（a，b）＝
，就称向量a与b垂直，记作a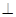
b。
注意，由于零向量与另一向量的夹角可以在0到之间任意取值，因此可以认为零向量与任何向量都平行，也可以认为零向量与任何向量都垂直。
当两个平行向量的起点放在同一点时，它们的终点和公共起点应在一条直线上。因此，两向量平行，又称两向量共线。
设有k（k≥3）个向量，当把它们的起点放在同一点时，如果k个终点和公共起点在一个平面上，就称为向量共面。
2．向量的线性运算
（1）向量加减法
①加减法则
a．三角形法则；
b．平行四边形法则。
（2）运算规律
向量的加法符合下列运算规律：
①交换律：a＋b＝b＋a；
②结合律：（a＋b）＋c＝a＋（b＋c）。
由于向量的加法符合交换律与结合律，故n个向量
（n≥3）相加可写成
。
设a为一向量，与a的模相同而方向相反的向量叫做a的负向量，记作-a。由此，我们规定两个向量b与a的差：
。
特别地，当b＝a有
。
由三角形两边之和大于第三边，有
及
，其中等号在a与b同向或反向时成立。
（3）向量与数的乘法
向量a与实数
的乘积记作a，规定a是一个向量，它的模
，它的方向为：当＞0时与a相同；当＜0时与a相反。当＝0时，
＝0，即a为零向量，这时它的方向可以是任意的。
向量与数的乘积符合下列运算规律：
①结合律：（
a）＝（a）＝（）a；
②分配律：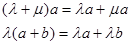
。
设
表示与非零向量a同方向的单位向量，那么
。
【定理】设向量a≠O，那么，向量b平行于a的充分必要条件是：存在唯一的实数，使b＝a。
3．空间直角坐标系
（1）坐标轴
在空间取定一点O和三个两两垂直的单位向量i，j，k，就确定了三条都以O为原点的两两垂直的数轴，依次记为x轴（横轴）、y轴（纵轴）、z轴（竖轴），统称为坐标轴。它们构成一个空间直角坐标系，称为Oxyz坐标系或[O，i，j，k]坐标系。
（2）坐标面
三条坐标轴中的任意两条可以确定一个平面，这样定出的三个平面统称为坐标面。x轴及y轴所确定的坐标面叫做xOy面，另两个由y轴及z轴和由z轴及x轴所确定的坐标面，分别叫做yOz面及zOx面。
（3）卦限
三个坐标面把空间分成八个部分，每一部分叫做一个卦限。含有x轴、y轴与z轴正半轴的那个卦限叫做第一卦限，其他第二、第三、第四卦限，在xOy面的上方，按逆时针方向确定。第五卦限至第八卦限，在xOy面的下方，第一卦限之下的为第五卦限，按逆时针方向确定，这八个卦限分别用字母Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ、Ⅶ、Ⅷ表示（图8-2）。
任给向量r，有对应点M，使
＝r，以OM为对角线、三条坐标轴为棱作长方体RHMK-OPAQ，如图8-3所示，有
图8-2 三个坐标面将空间分为八个卦限
图8-3 以OM为对角线的长方体RHMK-OPAQ
相关资料推荐
下一篇：
