找课后习题答案，就上大学教材课后答案网！
查看完整版：
高等数学第六版答案-高等数学第六版下册知识点总结
第8章 空间解析几何与向量代数
8.1 复习笔记
在平面解析几何中，通过坐标法把平面上的点与一对有次序的数对应起来，把平面上的图形和方程对应起来，从而可以用代数方法来研究几何问题。空间解析几何也是按照类似的方法建立起来的。
一、向量及其线性运算
1．向量概念
（1）向量
客观世界中有这样一类量，它们既有大小，又有方向，例如位移、速度、加速度、力、力矩等等，这一类量叫做向量（或矢量）。在数学上，常用一条有方向的线段，即有向线段来表示向量。有向线段的长度表示向量的大小，有向线段的方向表示向量的方向。以A为起点、B为终点的有向线段所表示的向量记
。有时也用一个黑体字母（书写时，在字母上面加箭头）来表示向量，例如a、r、v、F或
、
、
、
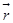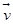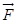等等。
（2）向量的大小和方向
由于一切向量的共性是都有大小和方向，因此在数学上只研究与起点无关的向量，并称这种向量为自由向量（简称向量），即只考虑向量的大小和方向。
由于只讨论自由向量，所以如果两个向量a和ｂ的大小相等，且方向相同，就认为向量a和ｂ是相等的，记作a＝ｂ。这就是说，经过平行移动后能完全重合的向量是相等的。
（3）向量的模
向量的大小叫做向量的模。向量、a、
的模依次记作
、
、
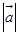。模等于1的向量叫做单位向量。模等于零的向量叫做零向量，记作0或
。零向量的起点和终点重合，它的方向可以看做是任意的。
（4）向量的夹角
设有两个非零向量a，b，任取空间一点O，作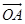
＝a，
＝b，规定不超过
的
AOB（设
＝AOB，0≤≤）称为向量a与b的夹角（图8-1），记作（a，b）或（b，a），即（a，b）＝。如果向量a与b中有一个是零向量，规定它们的夹角可以在0到之间任意取值。
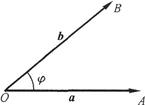
图8-1 非零向量a，b
如果（a，b）＝0或，就称向量a与b平行，记作a//b。如果（a，b）＝
，就称向量a与b垂直，记作a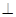
b。
注意，由于零向量与另一向量的夹角可以在0到之间任意取值，因此可以认为零向量与任何向量都平行，也可以认为零向量与任何向量都垂直。
当两个平行向量的起点放在同一点时，它们的终点和公共起点应在一条直线上。因此，两向量平行，又称两向量共线。
设有k（k≥3）个向量，当把它们的起点放在同一点时，如果k个终点和公共起点在一个平面上，就称为向量共面。
2．向量的线性运算
（1）向量加减法
①加减法则
a．三角形法则；
b．平行四边形法则。
（2）运算规律
向量的加法符合下列运算规律：
①交换律：a＋b＝b＋a；
②结合律：（a＋b）＋c＝a＋（b＋c）。
由于向量的加法符合交换律与结合律，故n个向量
（n≥3）相加可写成
。
设a为一向量，与a的模相同而方向相反的向量叫做a的负向量，记作-a。由此，我们规定两个向量b与a的差：
。
特别地，当b＝a有
。
由三角形两边之和大于第三边，有
及
，其中等号在a与b同向或反向时成立。
（3）向量与数的乘法
向量a与实数
的乘积记作a，规定a是一个向量，它的模
，它的方向为：当＞0时与a相同；当＜0时与a相反。当＝0时，
＝0，即a为零向量，这时它的方向可以是任意的。
向量与数的乘积符合下列运算规律：
①结合律：（
a）＝（a）＝（）a；
②分配律：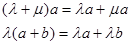
。
设
表示与非零向量a同方向的单位向量，那么
。
【定理】设向量a≠O，那么，向量b平行于a的充分必要条件是：存在唯一的实数，使b＝a。
3．空间直角坐标系
（1）坐标轴
在空间取定一点O和三个两两垂直的单位向量i，j，k，就确定了三条都以O为原点的两两垂直的数轴，依次记为x轴（横轴）、y轴（纵轴）、z轴（竖轴），统称为坐标轴。它们构成一个空间直角坐标系，称为Oxyz坐标系或[O，i，j，k]坐标系。
（2）坐标面
三条坐标轴中的任意两条可以确定一个平面，这样定出的三个平面统称为坐标面。x轴及y轴所确定的坐标面叫做xOy面，另两个由y轴及z轴和由z轴及x轴所确定的坐标面，分别叫做yOz面及zOx面。
查看完整版： 高等数学第六版答案-高等数学第六版下册知识点总结
相关资料推荐
下一篇：
